Confirmatory Factor Analysis (CFA)
Abstract
Confirmatory factor analysis (CFA) is a statistical technique used to validate the factor structure of a set of observed variables. It tests whether measured indicators reliably represent underlying latent constructs (Hair et al., 2018).
As demonstrated in the tutorial article on CFA/CB-SEM in SmartPLS by Hair et al. (2025), SmartPLS offers CFA capabilities as part of its covariance-based structural equation modeling (CB-SEM) functionality. With graphical model building and estimation based on maximum likelihood (ML), SmartPLS enables researchers to rigorously assess hypotheses about the relationships between observed and latent variables.
SmartPLS thus serves as a clear alternative to IBM SPSS Amos.
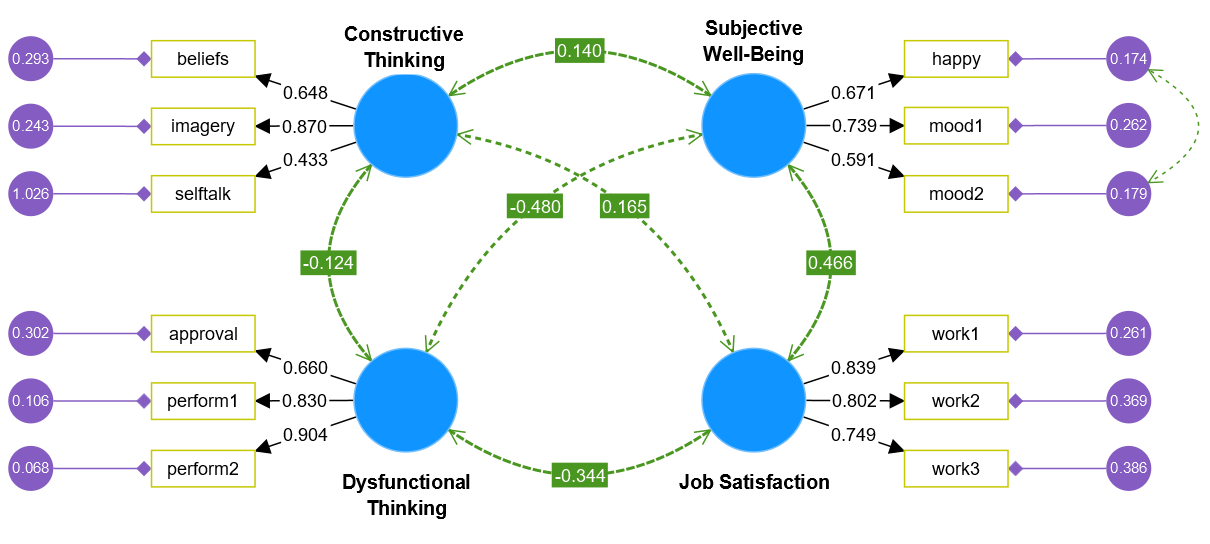
The following screenshot shows CFA results in SmartPLS for Kline’s (2023) textbook example on job satisfaction:
CB-SEM Algorithm Settings for CFA in SmartPLS
Maximum iterations
Defines the maximum number of iterations the optimizer will perform. This should be high enough to ensure convergence.
- Default value: 1,000
Starting value strategy
- Apply configured starting values
Uses user-specified starting values if enabled. Otherwise, default starting values are applied. - Default strategy
Mimics Lavaan’s defaults:- Loadings: Fabin-style estimates
- Path coefficients & covariances: 0.0
- Residual variances: 0.5 × indicator variance
- Latent variances: 0.05
- One-zero strategy
A simpler approach with:- Loadings: 1.0
- Variances: 1.0
- Path coefficients & covariances: 0.0
Stop criteria
- Gradient criterion
Optimizer stops when:||g|| < stop criterion × max(1, ||x||)- Default value: 10^-6
- Function value criterion
Optimizer stops when the improvement in the ML objective function is negligible:(f' – f) / f < stop criterion- Default value: 10^-9
Special assumptions
- Imply latent variable correlations
Estimates correlations between all exogenous latent variables, even without a correlation arrow. - Imply causal indicator correlations per construct
Estimates correlations between causal indicators of a latent variable, even without correlation arrows. - Imply a variance of 1.0 for causal indicators
Constrains all causal indicator variances to 1.0 (overrides user-specified values). Helps mimic Lavaan defaults.
Mean Structure
Most CFA and SEM analyses focus on modeling the covariance structure of observed variables. In some cases (e.g., latent growth curve modeling), including a mean structure is necessary. A mean structure involves means and intercepts of latent and observed variables and requires constraints for identification (since only p observed means are available, with p = number of observed variables).
Options
- No mean structure (default)
Ignores means and estimates only covariances. - Estimate mean structure, fix factor means to zero
Includes mean structure. Factor means are constrained to zero, while observed intercepts are estimated freely. - Estimate mean structure with only user-specified constraints
Includes mean structure with no predefined constraints. The user must specify identification constraints.
CFA Examples in SmartPLS
SmartPLS provides directly computable CFA examples from established textbooks (Byrne, 2016; Hair et al., 2018; Kline, 2023; Schumacker & Lomax, 2010). SmartPLS replicates the results reported in these sources. Try out the CFA example projects in SmartPLS!
References
- Byrne, B. M. (2016). Structural Equation Modeling with AMOS: Basic Concepts, Applications, and Programming (Multivariate Applications) (3 ed.). Routledge.
- Hair, J. F., Babin, B. J. Ringle, C. M., Sarstedt, M., & Becker, J.-M. (2025): Covariance-based Structural Equation Modeling (CB-SEM): A SmartPLS 4 Software Tutorial. Journal of Marketing Analytics, forthcoming.
- Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2018). Multivariate Data Analysis (8 ed.). Cengage Learning.
- Kline, R. B. (2023). Principles and Practice of Structural Equation Modeling (5 ed.). Guilford Press.
- Schumacker, R. E., & Lomax, R. G. (2010). A Beginner's Guide to Structural Equation Modeling (3 ed.). Routledge.
Cite correctly
Please always cite the use of SmartPLS!
Ringle, Christian M., Wende, Sven, & Becker, Jan-Michael. (2024). SmartPLS 4. Bönningstedt: SmartPLS. Retrieved from https://www.smartpls.com