Abstract

The Gaussian Copula approach allows researchers and practitioners to detect and correct for endogeneity in PLS-SEM (i.e., for relationships in the structural model).

Brief Description

While endogeneity can have various roots, such as measurement errors, simultaneous causality, common method variance, and (un)observed heterogeneity, endogeneity problems most often arise from omitted variables that correlate with one or more independent variable(s) and the dependent variable(s) in the regression model (Hult et al., 2018). Omitting such variables induces a correlation between the corresponding independent variables and the dependent variables' error term. That is, the independent variables then not only explain the dependent variable, but also the error in the model. In this context, we refer to the terms endogenous and exogenous to identify variables that endogeneity does (not) impact; we use dependent and independent to identify constructs that explain other constructs in partial least squares structural equation modeling (PLS-SEM), or are explained by them.

A straightforward way of handling, or at least reducing, endogeneity is to specify a set of control variables accounting for a part of the dependent variable's variance (Ebbes, Papies, & van Heerde, 2017). Despite their careful selection of control variables, researchers also need to apply a statistical approach to address endogeneity, if there could be a potential endogeneity problem. Two broad statistical approaches have been developed to examine the presence of endogeneity: instrumental variable and instrumental variable-free approaches (Papies, Ebbes, & van Heerde, 2017). While the instrumental variable approach has various disadvantage, the instrumental variable-free approaches offer several advantageous features (e.g., Hult et al., 2018). Amongst the instrumental variable-free approaches, the Gaussian copula method is particularly popular (Becker, Proksch, & Ringle, 2022; Park & Gupta, 2012).

There are two variants of the Gaussian copula approach. The original approach suggests the regression model's estimation by using an adapted maximum likelihood function that accounts for the correlation between the regressor and the error term using the Gaussian copula. The disadvantage of the maximum likelihood approach is that it can only account for one endogenous regressor in the model. In practice, almost all applications therefore use the second variant, which adds a "copula term" to the regression equation - like the control function approach for IV model estimation. This version has been implemented in SmartPLS. The Gaussian copula control function approach can also account for multiple endogenous regressors, which require the simultaneous inclusion of multiple copula terms, one for each regressor. This copula term's parameter estimate is the estimated correlation between the regressor and the error term scaled by the error's variance. On the basis of bootstrapped standard errors, a statistical test of this parameter estimate allows for assessing whether this correlation is statistically significant and endogeneity problems are therefore present (Hult et al., 2018; Papies, Ebbes, & van Heerde, 2017). A key requirement of for the application of the Gaussian copula approach is the nonnormality of the endogenous variable(s) (Park & Gupta, 2012), which and must be checked by researchers and partitions (e.g., via the Cramer-von-Mises nonnormality test); see also Becker et al. (2022). Also, in applications, the Gaussian copula has several additional limitations that require careful attention; for details, see Becker et al. (2022); Eckert and Hohberger (2022).

Hult et al. (2018) describe the detection and correction of endogeneity issues via the Gaussian copula approach and its use in PLS-SEM in more detail.

Gaussian Copula Apporach in SmartPLS

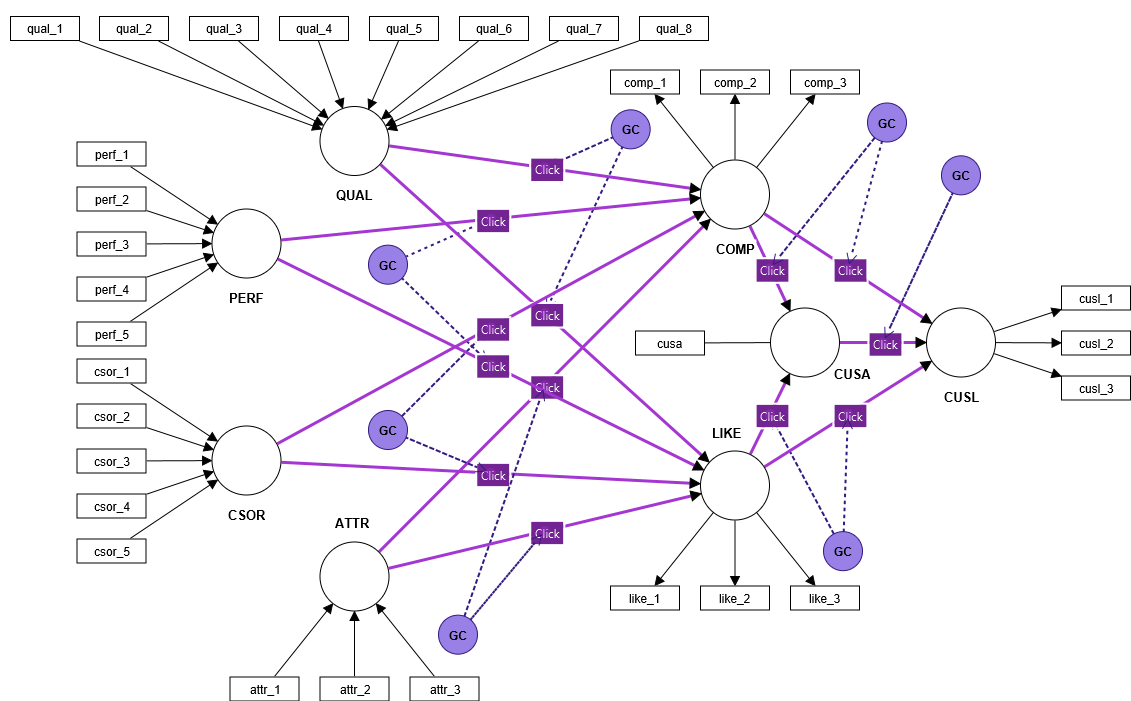
Create or open a PLS path model in SmartPLS. Click the Gaussian Copula button in the menu bar. The click-icon appears on each highlighted relationship in the structure model (see screenshot below). Now select the relationships in the structural model for which you want to detect and correct endogeneity problems using the Gaussian Copula approach. Left-click on the selected relation. As a result, a circle labeled GC appears in the model representing the additional Gaussian copula term for a relationship. Finally, use the PLS-SEM algorithm to estimate the model including the Gaussian copula terms and determine their significance using bootstrapping. Use these results to asses if critical endogeneity problems exist in the model that are corrected by the Gaussian copula terms.

Note: It is important that you check the requirements of the Gaussian Copula approach (e.g., non-normality of the endogenous variables) very carefully in each case (Becker et al., 2022).

References

Becker, J.-M., Proksch, D., and Ringle, C. M. (2022). Revisiting Gaussian Copulas to Handle Endogenous Regressors. Journal of the Academy of Marketing Science, 50: 46-66.

Ebbes, P., Papies, D., and van Heerde, H. J. (2017). Dealing with Endogeneity: A Nontechnical Guide for Marketing Researchers. In Handbook of Market Research, C. Homburg, M. Klarmann, and A. Vomberg (eds.), Handbook of Market Research, Springer: Cham.

Eckert, C., and Hohberger, J. (2022). Addressing Endogeneity Without Instrumental Variables: An Evaluation of the Gaussian Copula Approach for Management Research. Journal of Management, 01492063221085913.

Hult, G. T. M., Hair, J. F., Proksch, D., Sarstedt, M., Pinkwart, A., and Ringle, C. M. (2018). Addressing Endogeneity in International Marketing Applications of Partial Least Squares Structural Equation Modeling. Journal of International Marketing, 26(3): 1-21.

Papies, D., Ebbes, P., and van Heerde, H. J. (2017). Addressing Endogeneity in Marketing Models. In Advanced Methods in Modeling Markets, P. S. H. Leeflang, J. E. Wieringa, T. H. A. Bijmolt, and K. H. Pauwels (eds.), Springer: Cham, pp. 581-627.

Park, S., & Gupta, S. (2012). Handling Endogenous Regressors by Joint Estimation Using Copulas. Marketing Science, 31(4): 567-586.

More literature ...