Abstract

Standard conceptualizations that underpin cause-effect relationships in PLS path models imply that constructs affect another in a linear fashion. In some instances, however, this assumption does not hold in that relationships may be nonlinear.

Brief Description

In PLS-SEM, relationships between constructs can take various forms. While linear relationships can be represented by straight lines (with positive or negative slopes) when plotting the latent variables’ values in a scatterplot, nonlinear relationships include all associations that are not straight lines but curves.

When the relationship between two constructs is nonlinear, the size of the effect between two constructs not only depends on the magnitude of change in the exogenous construct but also on its value. In analyzing nonlinear effects, researchers have to make an assumption regarding the nature of the effect. While an abundance of different effect types is possible, quadratic effects are most common. The following figure shows the quadratic effect estimation of satisfaction on loyaltiy for the corporate reputation model in SmartPLS.

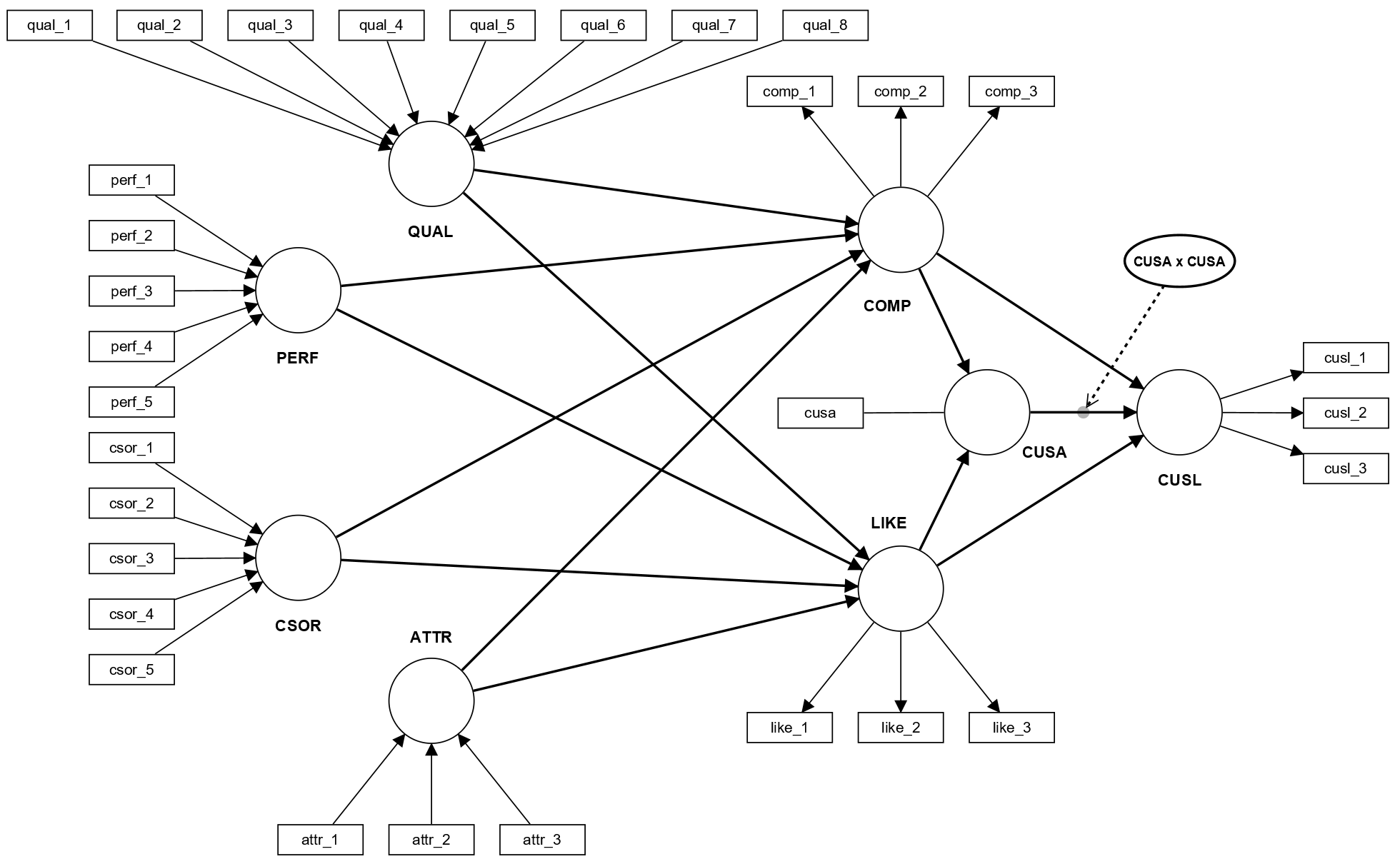
A nonlinear effect can be modeled as shown in the figure. To add the quadratic term, select the "Quadratic effect" option in the menu bar of the SmartPLS modeling window and click on the path relationship in the structural model to which you want to add the quadratic effect. Basco et al. (2021) and Hair et al. (2024) describe the analysis of quadratic effects and their use in SmartPLS in more detail. In fact, it is like a self-moderation (see also the explanations on moderation). The computation of results uses the two-stage approach. This approach uses the latent variable scores of the latent predictor variable from the main effects model (without the quadratic effect term). These latent variable scores are saved and used to calculate the squared indicator for the second stage analysis that involves the quadratic effect term in addition to the predictor variable (see also the explanations on moderation). For the quadratic effect resutls interpretation, please take a look at Basco et al. (2021) and Hair et al. (2024).

References

• Chin, W. W., Marcolin, B. L., and Newsted, P. R. 2003. A Partial Least Squares Latent Variable Modeling Approach for Measuring Interaction Effects: Results from a Monte Carlo Simulation Study and an Electronic-Mail Emotion/Adoption Study. Information Systems Research, 14(2): 189-217.

• Ahrholdt, D.C., Gudergan, S., and Ringle, C.M. 2019. Enhancing Loyalty: When Improving Consumer Satisfaction and Delight Matters. Journal of Business Research, 94(1): 18-27.

• Basco, R., Hair, J. F., Ringle, C. M., and Sarstedt, M. 2021. Advancing Family Business Research Through Modeling Nonlinear Relationships: Comparing PLS-SEM and Multiple Regression. Journal of Family Business Strategy, 100457.

• Becker, J.-M., Ringle, C. M., and Sarstedt, M. 2018. Estimating Moderating Effects in PLS-SEM and PLSc-SEM: Interaction Term Generation x Data Treatment. Journal of Applied Structural Equation Modeling, 2(2): 1-21.

• Hair, J. F., Sarstedt, M., Ringle, C. M., and Gudergan S. P. 2024. Advanced Issues in Partial Least Squares Structural Equation Modeling (PLS-SEM), 2nd Ed., Sage: Thousand Oaks.

• Rigdon, E. E., Ringle, C. M., and Sarstedt, M. 2010. Structural Modeling of Heterogeneous Data with Partial Least Squares. In Review of Marketing Research, N. K. Malhotra (ed.), Sharpe: Armonk, 255-296.

• More literature ...